Bezier curves are nothing new, and there is a lot of good code out there that implements them well. I started with Paul Burke's algorithm, mainly because someone had already ported it to Gideros. This algorithm works quite well, is fast, and is simple enough to understand. However, I thought I could figure out how to improve on my implementation at least a little, without switching to a much more complicated algorithm. My goals were to produce curves with points in all the optimal places resulting in it being smooth, but with as few points as possible. So this is what I've come up with.
First, here is my naive implementation.
Bezier = Core.class(Shape)
function Bezier:createCubicCurve(p1, p2, p3, p4, steps)
self.points = {}
steps = steps or 100
for i = 0, steps do
table.insert(self.points, self:bezier4(p1, p2, p3, p4, i/steps))
end
end
function Bezier:bezier4(p1,p2,p3,p4,mu)
local mum1,mum13,mu3;
local p = {}
mum1 = 1 - mu
mum13 = mum1 * mum1 * mum1
mu3 = mu * mu * mu
p.x = mum13*p1.x + 3*mu*mum1*mum1*p2.x + 3*mu*mu*mum1*p3.x + mu3*p4.x
p.y = mum13*p1.y + 3*mu*mum1*mum1*p2.y + 3*mu*mu*mum1*p3.y + mu3*p4.y
--p.z = mum13*p1.z + 3*mu*mum1*mum1*p2.z + 3*mu*mu*mum1*p3.z + mu3*p4.z
return p
end
This gives us 101 points for the cubic curve {100,100}, {800,250}, {800,100}, {150,200}. This isn't too bad, as it gives us enough for it to be smooth, but using way too many points. Much longer curves will end up with too-few points and could appear jagged, and much shorter curves will end up with too many.
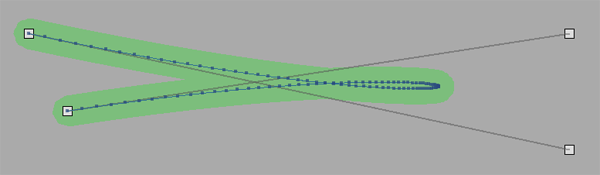
Automatic estimation of steps
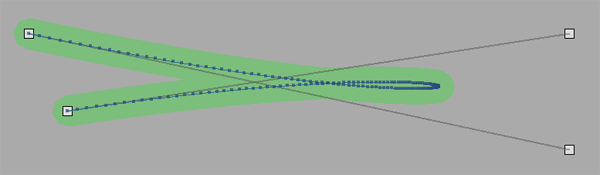
First, I wanted to figure out a way to estimate the number of steps for a given curve, based on it's length instead of just always using 100. This way shorter curves would have fewer points, avoiding unnecessary overhead, and longer curves would have more points, smoothing them out. The problem is, we don't really know the length until we actually calculate it. However, we can guess based on the distances of all of the points. Basically we estimate it at 10% (by default) of the total distance between all points. This seems to work fine in my tests. If you want more points, just increase the percentage.
function Bezier:estimateSteps(p1, p2, p3, p4)
local distance = 0
if p1 and p2 then
distance = distance + self:pointDistance(p1, p2)
end
if p2 and p3 then
distance = distance + self:pointDistance(p2, p3)
end
if p3 and p4 then
distance = distance + self:pointDistance(p3, p4)
end
return math.max(1, math.floor(distance * self.autoStepScale))
end
This gives us 153 points for this particular curve. This will help smooth out tight turns in curves much larger than this, but is way too many for most parts of the curve, such as the long straight parts. So by itself, this isn't much of a solution.
Reduction of points
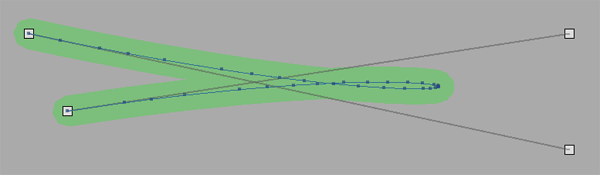
So the last thing I wanted to do was to get rid of unnecessary points. If a part of the curve is pretty much straight, we don't need so many points to somewhat accurately describe it. After some searching around I found the Ramer-Douglas-Peucker algorithm for reducing points in a curve, along with an implementation for Corona SDK. So now we can add a reduce() method. It recursively figures out redundant points that are less than epsilon distance from a line comprised of the current segment it's looking at. After it's done, we throw away all points that aren't marked as, "keep."
function Bezier:reduce(epsilon)
epsilon = epsilon or .1
if #self.points > 1 then
-- Keep first and last
self.points[1].keep = true
self.points[#self.points].keep = true
-- Figure out the rest
self:douglasPeucker(1, #self.points, epsilon)
end
-- Replace point list with only those that are marked to keep
local old = self.points
self.points = {}
for i,point in ipairs(old) do
if point.keep then
table.insert(self.points, {x=point.x, y=point.y})
end
end
end
function Bezier:douglasPeucker(first, last, epsilon)
local dmax = 0
local index = 0
for i=first+1, last-1 do
local d = self:pointLineDistance(self.points[i], self.points[first], self.points[last])
if d > dmax then
index = i
dmax = d
end
end
if dmax >= epsilon then
self.points[index].keep = true
-- Recursive call
self:douglasPeucker(first, index, epsilon)
self:douglasPeucker(index, last, epsilon)
end
end
function Bezier:pointLineDistance(p, a, b)
-- calculates area of the triangle
local area = math.abs(0.5 * (a.x * b.y + b.x * p.y + p.x * a.y - b.x * a.y - p.x * b.y - a.x * p.y))
-- calculates the length of the bottom edge
local dx = a.x - b.x
local dy = a.y - b.y
local bottom = math.sqrt(dx*dx + dy*dy)
-- the triangle's height is also the distance found
return area / bottom
end
This now gives us 34 points. It spreads them out on the straighter parts, but packs them in on the sharp corners so they will appear as smooth as the un-reduced version. So visually this is exactly what I wanted, but at what cost?
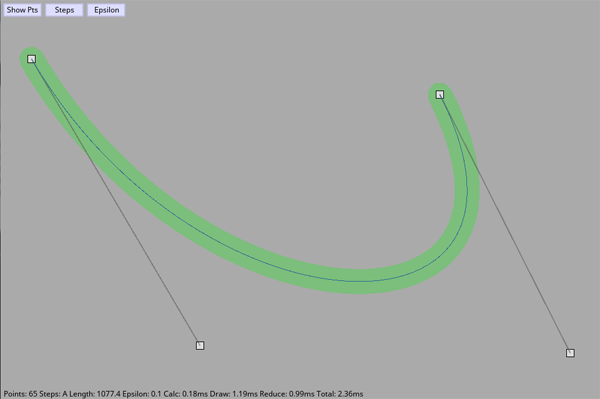
Performance
At first I expected these extra operations to slow everything down, but I figured it was worth it in certain cases. However, I was surprised to find that by far the slowest part of rendering the curve is actually having Gideros draw it as a series of connected lines. So while my reduce() function is expensive, because it reduces the number of points so much, the end result is less drawing, and so overall it's faster. Here are some benchmarks of the curve in the images above, running in the desktop player:
| Parameters | #points | Creation | Drawing | Reduction | Total |
|---|---|---|---|---|---|
| 100 steps, no reduce | 101 | 0.12ms | 1.94ms | 0.00ms | 2.07ms |
| Auto steps, no reduce | 153 | 0.21ms | 3.15ms | 0.00ms | 3.36ms |
| Auto steps, .1 epsilon | 34 | 0.21ms | 0.67ms | 0.82ms | 1.70ms |
Source
The full class and a test project is available at github.
Further
If you're interested in a different approach altogether, take a look at Maxim Shemanarev's paper, "Adaptive Subdivision of Bezier Curves." It is a much more complicated algorithm, but he gets beautiful results.
